模型校验是最成功的需求验证工具。模型校验的基本原理如图1所示。模型校验工具的输入是系统需求或设计(称为模型)以及最终系统期望实现的特性(称为“规范”)。如果给定的模型满足给定的规范,那么工具将输出yes,否则将生成反例。反例详细描述了模型无法满足规范的原因,通过研究反例,可以精确地定位模型的缺陷,如此反复。该方法的原理是通过确保模型满足足够多的系统特性以增强我们对模型正确性的信心。系统需求之所以称为模型,因为这些模型表征的是需求或设计。
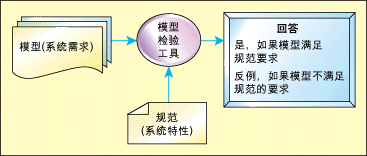
图1:模型校验方法。
那么,哪种规范化语言可以用来定义模型呢?答案当然不是唯一的,因为不同应用领域的需求(或设计)差异很大。例如,银行系统和空间系统在系统规模、结构、复杂度、系统数据的属性及执行操作上的需求差异就很明显。相反,大多数实时嵌入式或安全临界系统都面向控制,而不是数据,这意味着这些系统的动态特性远比业务逻辑(由系统维护的内部数据的结构及操作)重要。这些基于控制的系统可以应用于诸多领域:航天系统、航空电子、汽车系统、生物医学仪器、工业自动化及过程控制、铁路、核电站等。甚至数字硬件系统的通信和安全协议均可视为面向控制的系统。
对于面向控制的系统,可以采用有限状态机(FSM)定义需求和设计,这是一种得到广泛认可的抽象表示方法。当然,光靠FSM并不能对复杂的实际工业系统进行建模。我们还需要:1. 能将需求模块化并区分需求等级;2. 能合并各组成部分的需求(或设计);3. 能通过更新预先规定的变量和设备,防止可能出现的异常。
校验设计需求时,通常可以通过回答一些问题得到结果。下面给出了校验需求时最常问的一些问题:
* 设计需求是否准确地反映了用户需求?需求中的每一事项是否与用户的期望一致?需求是否包含用户所要求的全部内容?
* 设计需求是否表述清晰并无异义?是否能被用户很好地理解?
* 设计需求是否具有灵活性和可实现性?例如设计需求是否模块化并具有良好的架构,从而有助于设计和开发?
* 设计需求是否能轻松地定义验收测试示例以验证设计实现与需求的一致性。
* 设计需求是否只是概要地描述而与具体的设计、实现及技术平台等无关,从而使得设计人员和开发人员具有充分的自由度实现这些需求?
回答这些问题当然绝非轻而易举而且也没有任何捷径可循,但如果需求成功地超越了这些条条框框,那么无疑为优良系统的设计打下了坚实基础。尽管可以利用类似UML这样的建模工具,但仍然需要确保设计需求的质量。这个过程需要投入大量精力和时间,包括各种形式的审查,有时甚至还需要进行部分原型设计。此外,需求设计中采用多种表示方法(如UML中的表示方法)通常又将引发其他的问题,例如:
* 设计需求需要使用哪种表示方法?
* 如何确保不同表示方法的描述的一致性?
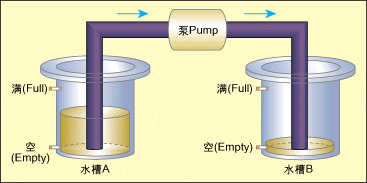
图2:简单的双水槽泵控系统。
设计需求缺陷的成本通常很高,至少需要重设计并进行维护。错误的需求导致错误的系统行为并显著增加成本,如丧失产品的时效性和本质特征,而对于工作在实时环境下的嵌入式安全临界系统更是如此。为确保系统设计的质量,也需要考虑类似的问题。
改进需求和设计的一条途径是利用自动化工具对需求和设计各环节的质量进行校验。那么,哪种工具最适用呢?一般而言,校验用英文描述的需求或设计极为困难。因此,必须采用一种清晰严格且无二义的规范化语言对需求进行描述。如果这种描述需求和设计的语言具有明确的语义,那么完全可以开发出自动化工具以分析这种语言描述的设计需求。这种采用严格语言描述需求或设计的基本思想已成为系统验证的基石。
简单的系统模型实例
首先,让我们考察一下如何利用模型校验工具验证简单的嵌入式系统特性。为此,我们采用Carnegie-Mellon大学开发的符号模型验证器(symbolic model verifier,SMV)作为模型校验工具。当然,我们也可以采用其他的模型校验工具描述该模型。文章结束部分列出了可选的模型校验工具及获取方式。
如图2所示,一个简单的泵控系统通过泵P将源水槽A中的水传送至接收水槽B。每个水槽都具有两级刻度线:一个用来检测水位是否为空(Empty),而另一个用来检测水位是否已满(Full)。如果水槽的水位既不为空也不为满,那么水槽刻度线设定为ok;换言之,即水位高于空刻度线但低于满刻度线。
最初,两个水槽均为空。一旦水槽A的水位值为ok(从空开始),启动泵并假定水槽B尚未为满。只要水槽A不为空且水槽B不为满,泵将持续工作。一旦水槽A为空或水槽B为满,泵将停止工作。一旦泵启动(或停止),系统将不会尝试停止(或启动)泵。虽然这个示例非常简单,但可以很容易地扩展为控制多个源水槽和接收水槽的复杂泵管线网络控制器,如应用在水处理系统或化工厂中的控制器。
表1:SMV模型描述和需求清单。
MODULE main
VAR
level_a : {Empty, ok, Full}; -- lower tank
level_b : {Empty, ok, Full}; -- upper tank
pump : {on, off};
ASSIGN
next(level_a) := case
level_a = Empty : {Empty, ok};
level_a = ok & pump = off : {ok, Full};
level_a = ok & pump = on : {ok, Empty, Full};
level_a = Full & pump = off : Full;
level_a = Full & pump = on : {ok, Full};
1 : {ok, Empty, Full};
esac;
next(level_b) := case
level_b = Empty & pump = off : Empty;
level_b = Empty & pump = on : {Empty, ok};
level_b = ok & pump = off : {ok, Empty};
level_b = ok & pump = on : {ok, Empty, Full};
level_b = Full & pump = off : {ok, Full};
level_b = Full & pump = on : {ok, Full};
1 : {ok, Empty, Full};
esac;
next(pump) := case
pump = off & (level_a = ok | level_a = Full) &
(level_b = Empty | level_b = ok) : on;
pump = on & (level_a = Empty | level_b = Full) : off;
1 : pump; -- keep pump status as it is
esac;
INIT
(pump = off)
SPEC
-- pump if always off if ground tank is Empty or up tank is Full
-- AG AF (pump = off -> (level_a = Empty | level_b = Full))
-- it is always possible to reach a state when the up tank is ok or Full
AG (EF (level_b = ok | level_b = Full))
该系统的模型的SMV建模如表1所示。起始的VAR部分定义了系统的3个状态变量,变量level_a和level_b分别记录了上层水槽(upper tank)和下层水槽(lowertank)的当前水位;在每个“时刻”,这两个变量都将分别赋值,取值范围为Empty、ok或Full。变量pump表征了泵的启动(on)和停止(off)。
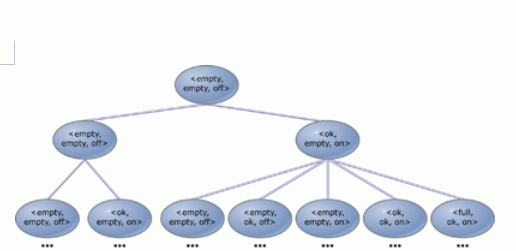
图3:泵控系统执行树的初始部分。
系统状态就可用上述3个变量的不同取值来表示。例如(level_a=Empty, level_b=ok, pump=off)和l (level_a=Empty, level_b=Full, pump=on)就可以表示系统状态。在靠近结尾的INIT部分,定义了这些变量的初始值(这里,最初假定pump的初始值为off,而其他两个变量则可取任意值)。
ASSIGN部分定义了系统如何从一个状态迁移到另一个状态。每个next语句都规定了特定变量的取值变化。所有这些赋值语句都假定可以并行执行;next语句定义为在该部分执行所有赋值语句后的最终结果。下层水槽的状态可以从Empty状态迁移到Empty或ok状态;从ok状态迁移到Empty或Full状态,或保持为ok状态(如果pump的状态为on);从ok状态迁移到ok或Full状态(如果pump的状态为off);如果pump状态为off,那么下层水槽在Full状态无法发生状态迁移;如果泵状态为on,则可迁移到ok或Full状态。上层水槽也可规定类似的操作。
在系统内部,大多数模型校验工具通常会将输入模型扩展为具有Kripke结构的动态系统。扩展过程包括在EFSM中除去分层结构、并行成分以及状态迁移时的告警和操作。Kripke结构中的每个状态实际上都可用每个状态均赋值的元组(tuple)来表示。Kripke结构中的状态迁移表征了一个或多个状态变量取值的变化;而且还可以比较通过扩展给定模型而得到的Kripke结构,对指定的系统属性进行校验。然而,为了更好地理解每条属性语句的含义,Kripke结构还必须进一步扩展为无限树形结构,其中树形结构的每个分支都表征了系统可能的执行操作或行为。
路径和属性规范
最开始,系统可以处于9个状态中的任意一个,其中对于A和B的水位没有任何限制,而pump的初始状态假定为off。这样,我们就可以利用有序元组表征状态,其中A和B分别表示水槽A和B的当前水位,而P则表示pump的当前状态。例如,可以假定系统的初始状态为。对于系统模型,初始状态之后的下一个状态可以为和中的任意一个。从状态开始,下一个状态可以为、、、、或中的任意一个。根据每个状态,可以计算出下一个可能的状态。
这些状态可以无限执行(或运算)树状结构的形式进行排列。如图3所示,树根为我们所选的初始状态,任意状态的分支均表示下一个可能的状态,而每个系统执行都是执行树状结构的一条路径。总体上,系统可以具有无限多个这样的执行路径。模型校验的目标就是检验执行树状结构是否满足用户指定的属性要求。
现在的问题在于,我们究竟该如何描述执行树状结构路径(及路径上的状态)的属性。从技术的角度看,运算树逻辑(Computation tree logic, CTL)是时序逻辑(time temporal logic, TTL)的一个分支,其简单性和直观性非常适合于本例。CTL是常用的布尔命题逻辑(Boolean propositional logic, BPL)的扩展,除了支持包括“和(and)”、“或(or)”、“否(not)”、“蕴涵(implies)”在内的BPL逻辑连接操作外,还支持辅助的时序连接操作。表2所示为 CTL 中的某些连接操作。
表1和图4说明了CTL中一些基本时序连接操作的直观意义。一般地,E(就某个路径而言)和A(就所有的路径而言)表示从某个状态开始的路径数目。F(就某个状态而言)和G(就所有状态而言)表示某个路径中的状态数目。
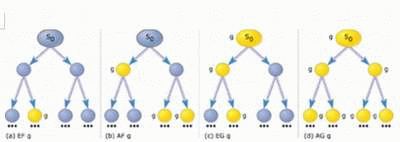
图4:状态s0处满足CTL公式的直觉推导。
对于指定的属性以及对应于系统模型的运算树T(可以是无限运算树),模型校验算法可以通过校验T判断T是否满足该属性。例如,考虑指定的属性AF g,其中g表示与任何CTL连接无关的命题公式。图4b给出了运算树T的一个示例。如果属性AF g在根状态s0的值设定为true(即如果T中的每条路径中有状态开始于s0以使公式g为true),那么对于该运算树TAF g的值为true。如果g在s0为true,那么就实现了预定目标,因为s0将会出现在从s0开始的每条路径中。但如果g在s0状态下不为true,由于从s0开始的路径要么是s0的左分支,要么是s0的右分支,因此如果在运算树T中s0的两个分支都为true(通过递归校验),那么该属性在s0处也为true。
图4b显示,g在左分支根部为true(球体填充为黄色)。因此从s0到左分支单元的所有路径以及整个左分支树都满足该属性。现在假定g在s0的右分支根部不为true;因此对于所有的子单元都将递归检验该属性。图4b显示,对于s0右分支的所有子单元,g都为true(球体填充为黄色),因此对于s0的右分支树该属性为true。这样,对于s0的所有子分支树该属性为true,从而s0也为true。
图4归纳了类似的其他属性(例如EG g和AG g)校验原理。当然,实际应用中的模型校验算法远比这复杂;这些算法利用一些巧妙的简化手段对状态空间进行精简,从而避免了对那些确保为true的属性进行校验。一些设计良好的模型校验器可用来校验状态数高达1,040个的状态空间的属性。在SMV中,待验证的属性可由SPEC部分的用户指定。逻辑连接“否”、“或”、“和”和“if-then”可以分别用!、|、&和 ->表示。CTL时序连接则表示为AF、AG、EF、EG等。属性AF(pump=on)表示对于每条开始于初始状态的路径,路径中有一个pump=on的状态。在初始状态,该属性显然为false,因为从初始状态开始有一条路径pump的值始终为off(例如,当水槽A永远保持为空时)。如果希望在SPEC部分中描述该属性,那么SMV将为该属性生成如下反例。循环表征了开始于初始状态的无限状态序列(换言之,即路径),这样水槽B在该路径下的每个状态均为Full,因此pump=off。
与严格的规范化语言相结合,可以下列执行序列表示:
state 1.1:
level_a = Full
level_b = Full
pump = off
state 1.2:
属性AF(pump=off)具有两重含义,表征的是对于每条开始于初始状态的路径,路径中有一个状态中pump=off。该属性当然在初始状态为true,因为初始状态本身(所有路径均包含初始状态)pump=off就成立。

表2:CTL中的一些时序连接。
时序连接和逻辑连接相结合,可以得到一些有趣的复杂属性。属性AG((pump=off) -> AF (pump=on))表示如果pump=off,那么最终pump=on这种情形总会发生。初始状态,该属性显然为false。属性AG AF (pump=off -> (level_a=Empty | level_b=Full))表示如果底层水槽为Empty或上层水槽为Full,那么pump将总是为off。属性AG (EF (level_b= ok|level_b=Full))表示总是会出现上层水槽为ok或Full的情形。
实际应用中的模型校验
模型校验已被证明是对各类系统(尤其是硬件系统、实时嵌入式系统和安全临界系统)进行需求和设计验证的有效工具。例如,SPIN模型校验器曾用于验证NASA的深空1发射方案中的多线程规划执行模型并成功地发现了5个先前未知的并发缺陷。然而,实际使用模型校验时还需要注意下面一些主要问题:
1. 每种模型校验工具都采用特有的建模语言,这些建模语言一般都无法将不规范的需求描述自动转化为规范化语言。这样的转化显然需要手工完成,因此很难检验模型是否正确地表示了建模系统。实际上,指定的建模表示法往往很难甚至根本不可能对部分系统需求进行建模。2. 专用工具属性规范表示法也存在类似的问题,属性表示法通常可以是CTL、CTL*或命题线性时序逻辑(PLTL)的变形。某些需要验证的属性很难甚至根本不可能用该表示法进行描述。3. 模型系统中的状态数量也可能极为庞大。尽管模型校验算法可以利用一些技巧减小状态空间的复杂度,但模型校验器仍然需要很长的时间才能验证一个指定的属性或者决定“放弃”验证该属性。这时,用户将不得不投入更大的精力,独立验证模型的各部分或者通过减小变量的取值范围以达到简化状态空间的目的。
尽管如此,模型校验仍被证明是无与伦比的系统需求或设计验证工具。该工具能在需求或设计的早期阶段发现瑕疵,因此能极大地节省后续的开发时间。
鸣谢
衷心感谢Tata研发和设计中心(TRDDC)的常务董事Mathai Joseph教授对我的大力支持。我也非常感激Manasee Palshikar博士对我的鼓励和支持。
参考文献
1. Clarke, Edmund M., Orna Grumberg, and Doron A. Peled. Model Checking, Cambridge, MA: MIT Press, 1999.2. Berard, Beatrice, Michel Bidoit, Alain Finkel, Francois Laroussinie, Antoine Petit, Laure Petrucci, Philippe Schnoebelen, and Pierre Mckenzie. Systems and Software Verification: Model-Checking Techniques and Tools, Berlin-Heidelberg: Springer Verlag, 2001.
3. Havelund, Klaus, Mike Lowry, and John Penix. "Formal Analysis of a Space-Craft Controller using SPIN," IEEE Transactions on Software Engineering, vol. 27, no. 8, Aug. 2001, pp. 749-765.
4. Clarke, Edmund M., Orna Grumberg, and Doron A. Peled. Model Checking, Cambridge, MA: MIT Press, 1999.
5. Berard, Beatrice, Michel Bidoit, Alain Finkel, Francois Laroussinie, Antoine Petit, Laure Petrucci, Philippe Schnoebelen, and Pierre Mckenzie. Systems and Software Verification: Model-Checking Techniques and Tools, Berlin-Heidelberg: Springer Verlag, 2001.
6. Havelund, Klaus, Mike Lowry, and John Penix. "Formal Analysis of a Space-Craft Controller using SPIN," IEEE Transactions on Software Engineering, vol. 27, no. 8, Aug. 2001, pp. 749-765.
7. Harel, David, and Michal Politi. Modeling Reactive Systems with Statecharts—The Statemate Approach. New York, NY: McGraw-Hill, 1998.
作者:Girish Keshav Palshikar
Tata研发和设计中心科学家
Email: girishp@pune.tcs.co.in