关键词:查找表 Tiger SHARC TS101 DSP 实时性
1.概述:
我们知道,在三角函数的运算中,涉及到大量倒数和平方根的运算。TS101的ALU指令中,提供了很方便的求倒数指令RECIPS和求平方根倒数指令RSQRTS,在一个指令周期内,可以完成求一个浮点数的倒数或者平方根倒数的运算。但是,在TS101中,倒数和平方根倒数指令仅仅提供了8位浮点的近似值,特别在小数点后位数比较多的情况下,误差比较大。并且,在很多计算过程中,随着运算步骤的增加,其误差也不断扩大,最终将会导致运算的结果远远偏离正常的数值。如果需要提高倒数和平方根倒数的运算精度,就需要用到收敛算法,这样就大大增加了运算的周期数,使得运算量骤增。在需要大量三角函数运算的场合,这么大的运算量就显得很不合适,大大占用了系统的运行时间。在ADSP的集成开发环境Visual DSP 3.5++中,生产商虽然提供了进行三角函数计算的库函数,并具可以得到很高的计算精度,但是它的运算周期却比较长,很多情况下并不能满足我们的要求。
ADSP TS101中提供了专用的加法器和乘法器,使得高精度的乘加运算可以在一个周期内得以完成。如果我们可以利用乘加运算代替大运算量的求倒数和求平方根运算,那么程序运行中就可以大大降低程序的时间消耗。而且,三角函数具有一定的周期性,我们可以通过三角函数周期性的变换,将角度值变换到一个周期内,通过查表的方式来获得三角函数的数值。这种方式直接利用了三角函数的周期性,其误差大小决定于查找表的大小,也就是对一个周期内三角函数的数值进行采样的密度。在误差允许的情况下,可以以很高的运算速度得到三角函数的数值。
2.算法理论与DSP实现:
(1)DSP算法:正弦和余弦函数是按照2π为周期周期性变化的函数。对于 和 形式的函数,当我们知道x的数值以后,就可以根据浮点数x的小数部分的数值求得函数的数值,而整数部分可以作为周期循环的部分不予考虑。所以运算的重点在于如何将小数部分的数值转变为查表时候所对应的地址单元。我们取余弦函数 区间上的数值,在允许的计算精度范围内首先对其进行采样。因为余弦函数为偶函数,所以在整个自变量变化的范围内的三角函数运算都可以转变到 区间内进行。
对于三角函数 的数值的计算,我们将其自变量x的取值区间以0为中心分为小于零和大于等于零两部分。对于小于零的区间,首先求出x的绝对值,然后减去0.5,将得到的结果用fix指令求整,再用float指令将其表示为浮点数,将x的绝对值与用float指令求得的数值相减就提取出了数据的小数部分。对于大于零的区间,我们不用求其绝对值就可以直接按照上面的步骤提取出其小数部分。对于正弦函数 ,由于正弦函数是奇函数,情况就相对比较复杂一些。这时需要判断x的数值是大于零等于零还是小于零,如果在大于零的情况下,可以直接将小数部分提取出来,并对其进行查表得到对应的三角函数的数值,而在x的数值小于零的情况下,我们需要将在 区间内查表得到的数值再对其取负才可以得到相应的三角函数的数值。我们得到小数部分的数值以后,将小数部分的数值和采样的样本点数进行乘法运算,就可以得到查表所需要的相对地址。 查表实现的简单的汇编语言算法实现如下(未优化):
xr11=0.5;;
xfr20=abs r19;;
fr21=r20-r11;;
xr22=fix fr21;;
xfr23=float r22;;
xfr4=r20-r23;;
xfr5=r4*r3;; //r30 查找表采样样本点数
xr6=fix fr5;;
j3=xr6;;
xr1:0=l[j30+j3];; //j30 查找表绝对地址
(2)查找表样本制作和复指数信号的查表:在我们进行科学计算时,经常要碰到 形式的复指数运算,由欧拉公式我们可以得到 。在我们得到x的值之后,可以对 和 一起进行查表,从而得到相应的三角函数数值。TS101种,每次可以对4个word进行寻址操作。所以,我们在之前制作查找表的时候,对一个周期内的正弦和余弦函数采样之后,可以将正弦和余弦函数的查找表交叉存放。以64bit为单位,低32bit存放余弦函数的查找表数值,高32bit存放正弦函数的查找表数值。这样,在我们每次得到一个x的小数位数值之后就可以直接查找到两个函数的三角函数值,从而得到 的数值,极大的方便了复指数的运算。而且,采用TS101的单周期多指令方式,我们可以实现一个程序循环内并行查找多个复指数信号数值的操作,从而将速度大大提高。
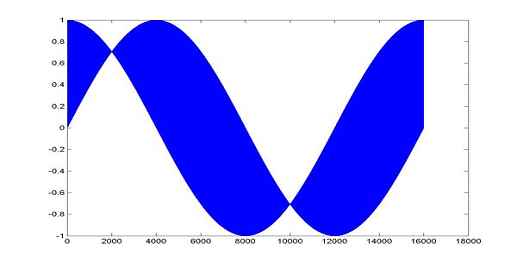
在我们进行查找表运算的时候,因为函数是周期性变化的,所以往往涉及到很多边界点的问题。在我们提供的这种算法中,对于x的数值为0的情况下,根据我们提供的算法,这个时候最后提取的数值为1。这是一个很特殊的边界点,在我们进行运算的时候必须将它的影响考虑进去,否则将会影响运算的结果。我们可以利用一种很简单的方法,就是在我们制作查找表的时候,将这种情况考虑进去。对采样的区间取 而不是 。这样,在我们进行查表运算的时候就可以避免边界点错误情况的出现。
3.误差分析
利用查找表进行三角函数的运算是一种近似的算法。由于我们是对一个周期之内的三角函数进行的采样,最终的结果必定会存在一种误差。误差的来源源自于两个方面,一个是采样存在的误差,一个是在进行查表运算的时,计算表地址的时候由于需要对数值取整,会引入一定的误差。这些误差的大小直接决定了我们所需要的查找表的大小,下面我们就对信号处理中经常用到的线性调频信号脉冲压缩的性能的影响来看一下该查表算法的精确度。(查找表采样长度16k)

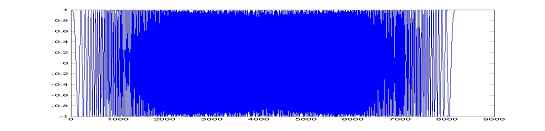
图二:查表数据与标准三角函数数据对比
(上图为标准实部数据,下图为查表所得实部数据)
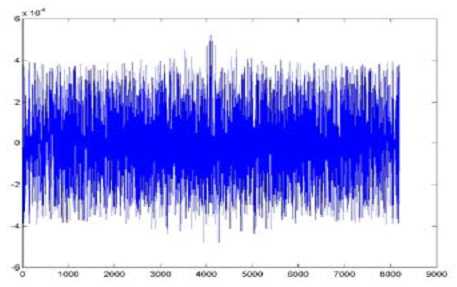
图三:绝对误差示意图
我们看到,在查找表采样点为16K的情况下,理论上的最大相对误差为: 2 * 2 * 2 / 16384 = 4.8828 *10^(-4)。。我们运算得到的最大相对误差约为 5.2 * 10 ^ (-4),在精度不是要求十分高的情况下,已经可以完全满足我们的需要。
在经过脉冲压缩之后对比,经过验证可以看出。两者的结果的误差已经十分小,完全达到了可以忽略的地步。
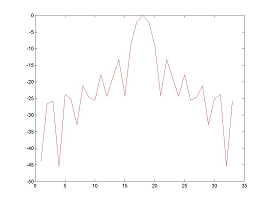

图四:脉冲压缩结果比较(dB)
4.运算量大小比较
在ADSP集成开发环境Visual DSP 3.5++中进行开发时,通过调用系统提供的库函数计算正弦和余弦函数的时候,所耗用的周期个数最少为20个周期,最多为58个周期,可以提供40bit的计算精度。在我们提供的算法中,虽然精度不能够达到这么高,但是可以在35个周期内计算2个复指数信号的函数值,也就是4个三角函数的数值。连续运算,可以达到38个周期,对2个复指数信号的运算。可以看出,我们虽然牺牲了三角函数的精度,但是却得到了很高的运算速度。在很多的计算场合下,我们并不需要得到十分精确的三角函数数值,只需要保证计算得到的函数规律在误差允许的范围内就可以。这时候,本文提供的查表运算可以保证有比较好的实时性。
利用这种查找表的方式进行三角函数的运算,优点在于运算的速度比较快,在精度要求不是很高的情况下,可以达到比较高的运算速度。当然,对于速度上的要求必然也会影响到处理的精度和误差。如果对于三角函数的数值要求有比较高的精度,那么这种查表的方式就显得不适合。这样,我们所允许的误差的大小,也就决定了我们所需要的查找表的大小。
5.结论
笔者在这里只是介绍了一种以查找表方式进行三角函数运算的方法,在笔者所需的实时运算要求下,可以达到所需的要求。实际上该算法还有可以改进和值得优化的地方,比如(1)查找表缩小到 区间内,根据函数的周期性,可以把运算统一到 的区间内,在采样点数不增加的情况下,而提高精度。(2)TS101种,提供了三个Bank的内部存储空间,每块存储空间的大小分别为2Mbit。如果我们的查找表比较大,占用了很大的内存空间的话,在最终程序修订,并需要通过主控计算机或者EPROM加载的时候,就会增大加载的文件的大小。所以,我们需要在查表的大小和精度、误差、程序占用空间大小方面取一个权衡,来决定查表的大小和计算的精度。
笔者在这里介绍的是一种在本人实际工程经验中所采用的三角函数的计算方法,望不足之处读者能够给与指出与修正。
联系E_mail: batistuta810226@sina.com