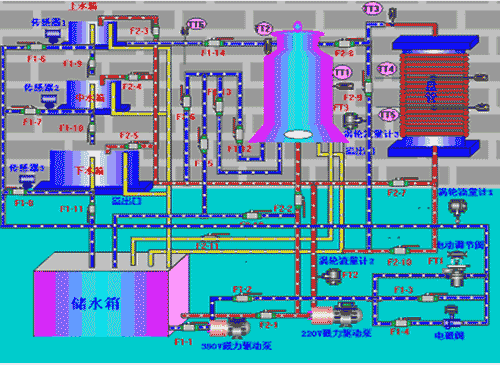
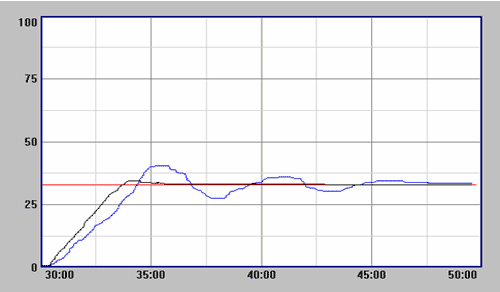
在工业生产中, 液位控制设备有着广泛的应用。在供液设备中, 液位控制又是其中的一个关键环节。自动液位控制的准确性和可靠性, 直接影响到供液设备的安全和供液质量。因此,设计自动液位控制器应本着工作稳定,控制准确,使用安全,操作方便的原则来进行。CMAC神经网络,即小脑模型,具有处理非线性和自学能力的特点,而且学习速度快。自1987年Miller等人成功地将其应用于机器人实时轨迹跟踪控制以来,小脑模型倍受关注。基于这种结构的控制器在阶跃输入或跟踪方波信号时,具有输出误差小、鲁棒性强等特点,然而在跟踪连续变化信号时,却容易产生过学习现象,进而导致系统的不稳定。为此,本文提出一种新型的CMAC控制器学习算法,并将其应用于位置伺服系统的非线性控制中.仿真结果表明,新型控制器具有很强的处理非线性和跟踪连续变化信号的能力,而且可以使用较高的学习速率,学习速度快,适于在线学习控制。
1. 小脑神经网络控制
CMAC网络由输入层、中间层和输出层组成。在输入层对n维输入空间进行划分。中间层由若干个基函数组成,对任意一个输入只有少数几个基函数的输出为非零值,称非零输出的基函数为作用基函数,作用基函数的个数为泛化参数c,它规定了网络内部影响网络输出的区域大小。中间层基函数的个数用p表示,泛化参数c满足c<<p 。在中间层的基函数与输出层的网络输出之间通过连接权ω进行连接,采用遗传算法实现权值的调整。CMAC的输入输出非线性关系由概念映射和实际映射来实现。结构如图1所示
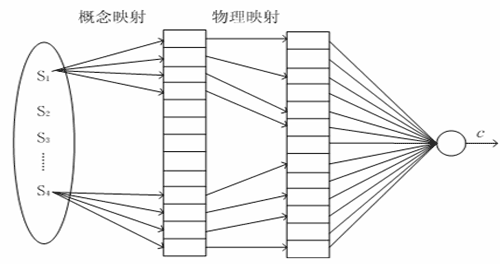
图1 CMAC结构图
2.学习算法
遗传算法借助搜索机制的随机性,能够搜索问题域的全局最优化解,并且对噪声和变化表现出很好的健壮性和自适应能力。故可以利用遗传算法确定该控制器物理存储器中的权值。学习算法如下:
(1)初始化:随机产生每个个体的染色体,在这个设计中用二进制编码,把Kp, Ki, Kd 3个参数分别表示成一串二制码,再依次连成一串二进制码,这样便可以用一个个体方便的表示出系统的参数集,从而可以简单的用遗传算法对系统的多个参数寻优。
(2)选择与交叉:首先计算个体对应变量值(二进制编码到变量的映射),
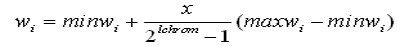
其中minwi是比例系数可能取到的最小值,maxwi是比例系数可能取到的最大值,lchrom是染色体的长度,x是wi所对应的二进制码的数值。
计算适应度,把控制器的参数代入控制系统,便可得各种输入下的系统响应,个体的适应度分别按下式计算:
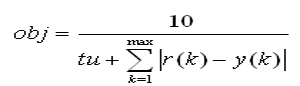
其中tu为上升时间,obj为个体适配值。
统计具有最大适应度的个体,累计一代的所有个体的适应度,并取每个个体的适应度与这一代所有个体适应度的比值作为该个体的选择概率。按适应程度从上一代选择两个个体,进行交叉,本文采用均匀交叉,即对所选的一对个体的每个对应二进制位按交叉概率进行一次交换,交叉概率是指定的。
(3)变异:新产生的个体的每一位按一定的概率进行一次变异,也就是跳变(原来是1变成0,0变成1)。概率也是指定的。
(4)重复执行上述步骤直到满足条件。
3.控制器结构及控制算法
基于遗传小脑子神经网络的控制器结构如图2所示,由图可以看出,该CMAC控制器平行地加在PD控制器之上,其结构与Miller的控制结构类似,但是它改变了CMAC的激励信号,即以系统的动态误差作为输入,以CMAC的输出与输入差通过遗传算法来调整权重。这样可以消除原有控制方案中累积误差的影响,进而消除系统的过学习现象。其工作可分为两个过程:控制与学习。其原理是,初始状态CMAC的所有权值。控制时,将下一步的误差期望值 e(K-1)(通常为0)与系统的当前误差e(k)量化后作为地址输入到CMAC,在CMAC存储器中找到与之对应的c个地址,并将这c个地址中的权重值相加,得到CMAC的输出,然后与PD控制器的输出Um相加,得到被控对象总的控制输入,即控制量。
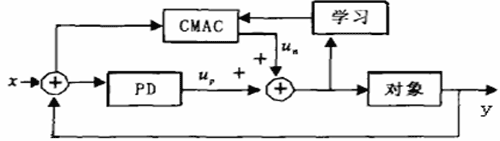
图2 遗传CMAC控制器
4.仿真研究
THJ-3型高级过程控制对象中的二容水箱可以模拟现场的二阶水位控制系统,其中的盘管可以模拟现场中的大滞后。控制对象如图3所示,